TP N°9
Les Arbres
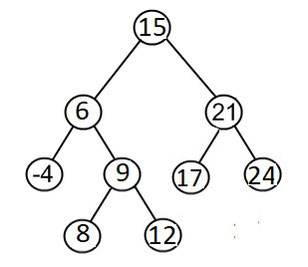
Exercice 1
Ecrire les fonctions, sur les arbres binaires de recherche (ABR Binary Search Tree BST), suivantes :
1. Parcours d’un arbre en préfixé, infixé puis en postfixé.
2. La recherche d’une valeur donnée dans un arbre et retourne l’adresse de l’élément précédent
3. L’insertion d’une valeur dans un arbre
4. La construction d’un arbre de n valeurs entières données. Les valeurs doivent être donné en commençant par la racine, ensuite le 1er niveau de gauche à droite, ensuite le 2eme niveau de gauche à droite et ainsi de suite et le programme vas inserer ces valeurs dans les noeuds correspondants.
5. L’affichage des éléments d’un arbre (en utilisant les 3 parcours)
6. L’affichage des feuilles (leaves) de l'arbre.
7. Le calcul du nombre de nœuds de l’arbre
8. Le calcul de la hauteur de l’arbre.
9. Déterminer si l’arbre est équilibré (balanced tree) ou non.
10. Calcul de la plus petite valeur (minimum) de l'ABR. Ecrire fonction récursive et fonction itérative.
11. Calcul de la plus grande valeur (maximum) de l'ABR. Ecrire fonction récursive et fonction itérative.
12. Etant donné une valeur val, affiche le chemin à partir de la racine jusqu'a une feuille dont la somme des noeuds est égale à val si un tel chemin existe.
13. Affiche tous les chemins à partir de la racine jusqu'a chacune des feuilles (idee: fonction void afficherTousLesChemins(bstNode *p) utilisera une fonction récursive auxiliaire afficherCheminRecur(bstNode *node, int cheminTab[], int cheminLen) en lui passant un tableau cheminTab[] et un entier cheminLen avec appel initiale comme: afficherCheminRecur(p, cheminTab, 0) et on supposera que le chemin ne peut avoir plus de 1000 noeuds. La fonction récursive mettera dans le tableau les noeuds qu'elle parcourt et affichera le chemin lorsqu'une feuille est atteinte.)
14. La suppression d’un nœud, voir ci-dessous pour la suppression d’un nœud.
15. Fonction récursive qui libère l'espace occupé par tous les noeuds d'un arbre ABR (void libererBSTRec(bstNode *p)).
16. Après construction de l’arbre recherche d’une valeur donnée dans l’arbre
17. Aussi après construction de l’arbre, insertion d’une nouvelle valeur val donnée ou bien la suppression d’un nœud et afficher l’arbre après insertion/suppression.
18. Fonction récursive qui crée un ABR equilibré à partir d'un tableau trié par ordre croissant. Idée; Prendre l'élément au milieu du tableau et le mettre comme la racine du ABR, puis refaire la meme chose avec la moitié droite du tableau et la partie gauche du tableau (bstNode *tabTrieAEquilBST(int T[], int debut, int fin))
19. Main pour tester toutes les fonctions précédentes.
Suppression d’un nœud
On peut résumer la suppression d’un noeud comme ci-dessous :
1. Suppression d’une feuille : Libérer l’espace occupé par le nœud et mettre à jour le lien gauche ou droit du précédent (dépendamment si le nœud est superieur ou inferieur au précédent) comme NULL, si le précédent existe. Si le précédent n’existe pas alors l’arbre devient vide.
2. Suppression d’un nœud qui a un seul descendant, Libérer l’espace occupé par le nœud et mettre à jour le lien gauche ou droit du précédent (dépendamment si le nœud est superieur ou inferieur au précédent) comme pointant vers le descendant, si le précédent existe . Si le précédent n’existe pas alors l’arbre est réduit au descendant du nœud à supprimer qui devient la racine.
3. Suppression d’un nœud qui a 2 descendants : remplacer la valeur du nœud à supprimer par la valeur du nœud le plus petit du sous arbre droit (SAD), c.a.d le nœud le plus à gauche du sous arbre droit et supprimer le nœud le plus à gauche du SAD, de cette façon on aura toujours un arbre binaire de recherche. Noter que le nœud le plus à gauche du SAD soit ça sera une feuille (cas 1) soit il aura un seul descendant (cas 2). Il faut noter aussi qu’on peut remplacer la valeur du nœud à supprimer par la valeur du nœud le plus grand du sous arbre gauche (SAG), c.a.d le nœud le plus à droite du SAG.
Exercice 2
Ecrire les fonctions suivantes:
1. Une fonction qui cherche la valeur minimale de l'ABR.
2. Une fonction qui cherche la valeur maximale de l'ABR.
3. Une fonction qui cherche le successeur d'un noeud p qui a une valeur val. Le successeur d'un noeud p est le noeud (s'il existe) dont la valeur est la plus petite parmi les noeuds qui ont une valeur plus grande que la valeur du noeud p en question. Idee: Si on a un noeud p alors s'il y'a un sous arbre a droite de p, tous les elements de ce sous-arbre sont plus grand que le noeud p et celui qui a la plus petite valeur est celui situe le plus a gauche dans ce sous arbre. Si le le noeud p n'a pas de sous arbre droit alors il faut remonter dans l'arbre (chercher le parent de p et de maniere iterative) jusqu'a arriver a une parent qui a un sous arbre gauche.
4. Une fonction qui cherche le predecesseur d'un noeud p qui a une valeur val. Le predecesseur d'un noeud p est le noeud (s'il existe) dont la valeur est la plus grande parmi les noeuds qui ont une valeur plus petite que la valeur du noeud p en question. Utiliser la meme idee que precedemment sauf que gauche devient droit et droit devient gauche.
Exercice 3
Ecrire les fonctions suivantes:
1. Une fonction qui cree un arbre binaire qui n'est pas un arbre binaire de recherche (non ABR).
Une maniere simple de creer un tel arbre est contrairement a un ABR d'inserer les valeurs > valeur courante a gauche du noeud courant et d'inserer les valeurs < valeur courante a droite du noeud courant. Une autre maniere de faire cela est d'alterner les insertions (fct insererNoeud1()). Une fois l'ordre inverse a un ABR et une fois comme un ABR. Implementer une telle methode.
2. "int minTreeValue(Node *p)": fonction recursive qui retourne le minimum d'un arbre binaire quelconque.
3. "int maxTreeValue(Node *p)": fonction recursive qui retourne le maximum d'un arbre binaire quelconque.
4. "int isBST1(Node *node)": fonction recursive qui indique si un arbre binaire est un ABR. Utiliser l'idee suivante: Un arbre binaire n'est pas un ABR si le max du SAG (Sous Arbre Gauche) est plus grand que le noeud courant, ou bien si le min du SAD (Sous Arbre Droit) est plus petit que le noeud courant, ou bien si le SAG n'est pas un ABR, ou bien si le SAD n'est pas un ABR. Dans tous les autres cas c'est un ABR. Utiliser les fonctions minTreeValue() et maxTreeValue().
5. "int isBST2(Node *node, int min_val, int max_val)": fonction recursive qui indique si un arbre binaire est un ABR. Dans la fonction isBST1() les memes noeuds sont traverses plusieurs fois lorsqu'on recherche le min du SAD et le max du SAG. Le but ici est de traverse les noeuds une seule fois. L'idee ici est lorsqu'on est a un noeud donne la valeur maximale des elements qui sont dans le SAG est la valeur courante du noeud - 1. De meme la valeur minimale des elements qui sont dans le SAD est la valeur courante du noeud + 1. Pour la racine il n'y a pas de min ou de max donc on peut utiliser comme min le minimum qu'un entier peut prendre et le maximum qu'un entier peut prendre. En C le fichier limits.h qui fait partie de la librairie C contient les valeur INT_MIN et INT_MAX qui sont de telles valeurs.
6. "int isBST3(Node *node)": fonction recursive qui indique si un arbre binaire est un ABR. Utiliser l'idee suivante: un arbre est un ABR si lorsque l'arbre est traverse en inorder (infixe) les elements sont tries par ordre croissant. Donc il faudra traverser l'arbre en inorder (infixe) et sauvegarder les elements dans un tableau. L'arbre est un un ABR si le tableau est trie par ordre croissant. Avant cela il faudra compter le nombre d'elements dans l'arbre pour allouer le tableau dynamiquement.
7. "int isBST4(Node *node)": fonction recursive qui indique si un arbre binaire est un ABR. Utiliser la meme idee que precedemment mais ne pas sauvegarder les elements dans un tableau. L'arbre est un ABR si pour tous les elements (sauf le premier) en ordre inorder (infixe) l'element courant est plus grand que le precedent. Donc il faudra sauvegarder quelque part le precedent. Noter que le premier element (c.a.d l'element le plus a gauche de l'arbre) il n'y a pas de precedent. Donc on peut utiliser un pointeur vers le precedent initialise a NULL lorsqu'on parcourt l'arbre en infixe. Ce pointeur sera mis a jour chaque fois qu'un neoud est traverse en infixe et pour le premier element il est egale a NULL.
8. "void arbreBinConvertABR(Node *p)": fonction qui convertit un arbre quelconque en ABR. Utiliser l'idee suivante: compter combien d'elements l'arbre contient et allouer un tableau d'entier d'autant d'elements. Traverser l'arbre en inorder et sauvegarder dans le tableau les elements dans cet ordre. Trier le tableau par ordre croissant. Remettre les elements du tableau dans l'arbre en faisant un parcours en inordre de l'arbre.
9. Ecrire le main() en creant un arbre quelconque (avoir plus qu'un noeud). Appeler les 4 fonctions isBST1(), isBST2(), isBST3() et isBST4(). Les 4 fonctions devront retourner 0 pour indiquer que ce n'est pas un ABR. Appeler la fonction arbreBinConvertABR() pour convertir l'arbre en ABR. Appeler de nouveau isBST1(), isBST2(), isBST3() et isBST4(). Maintenant les 4 fonctions doivent retourner 1 pour indiques que l'arbre est un ABR.
